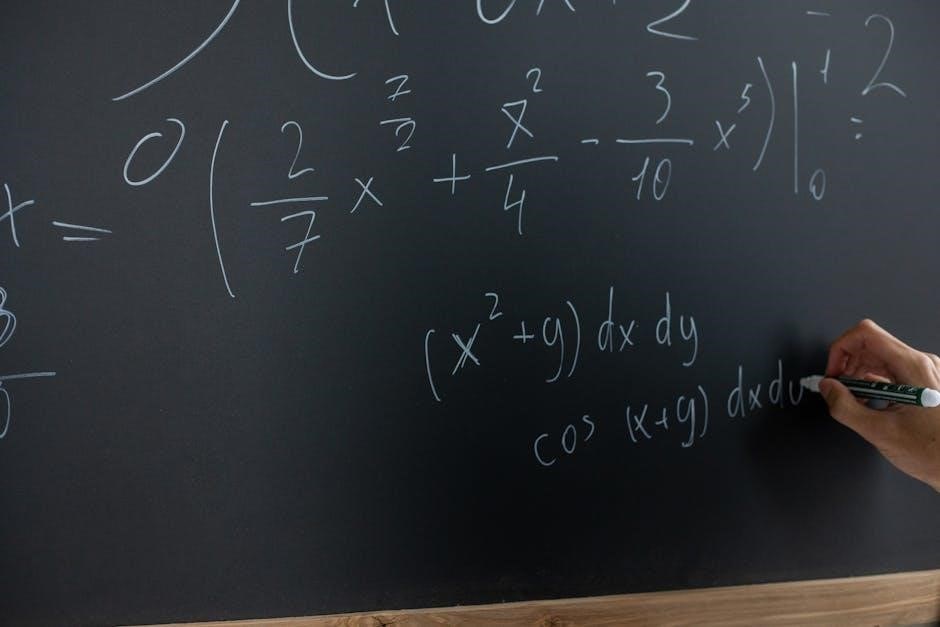Calculus is a fundamental field of mathematics exploring change and accumulation through graphical‚ numerical‚ and algebraic methods. These interconnected approaches provide a comprehensive understanding of complex problems‚ emphasizing the Rule of Four.
Overview of Calculus and Its Significance
Calculus is a cornerstone of mathematics‚ focusing on the study of change and accumulation. It is divided into differential and integral calculus‚ examining rates of change and slopes of tangents‚ as well as accumulation of quantities and areas under curves. The significance of calculus lies in its ability to model real-world phenomena‚ such as motion‚ growth‚ and optimization‚ making it indispensable in fields like physics‚ engineering‚ and economics; By blending graphical‚ numerical‚ and algebraic approaches‚ calculus provides a robust framework for understanding complex problems. Its applications extend to solving practical challenges‚ from predicting population growth to designing efficient systems‚ highlighting its profound impact on modern science and technology.
The Role of Graphical‚ Numerical‚ and Algebraic Methods
Graphical‚ numerical‚ and algebraic methods are essential tools in calculus‚ each offering unique insights into solving mathematical problems. Graphical methods visualize functions and their properties‚ aiding in understanding behavior and relationships. Numerical methods provide approximations‚ especially useful when exact solutions are difficult to obtain. Algebraic methods‚ on the other hand‚ offer precise formulations and solutions‚ solidifying conceptual understanding. Together‚ these approaches allow for a deeper exploration of calculus concepts‚ such as limits‚ derivatives‚ and integrals. By integrating these methods‚ students can approach problems from multiple perspectives‚ enhancing their ability to analyze and solve real-world challenges effectively. This multi-faceted approach is a cornerstone of modern calculus education‚ as emphasized in textbooks like Calculus: Graphical‚ Numerical‚ Algebraic by Ross L. Finney and others.
The Rule of Four: Connecting Different Representation Methods
The Rule of Four emphasizes the importance of understanding mathematical concepts through four interconnected representations: graphical‚ numerical‚ algebraic‚ and verbal. This approach‚ highlighted in textbooks like Calculus: Graphical‚ Numerical‚ Algebraic‚ ensures a holistic understanding of calculus. Graphical methods visualize relationships‚ numerical methods provide approximations‚ algebraic methods offer precise solutions‚ and verbal explanations reinforce conceptual clarity. By integrating these perspectives‚ students can tackle problems more effectively‚ as each method complements the others. This multi-faceted approach is particularly valuable for exploring complex calculus concepts‚ such as limits and derivatives‚ and fosters a deeper‚ more intuitive grasp of mathematical principles.

Graphical Methods in Calculus
Graphical methods involve visualizing functions and their properties to explore key calculus concepts. Tools like graphing calculators aid in analyzing limits and derivatives through graphical representations.
Visualizing Functions and Their Properties

Visualizing functions and their properties is a cornerstone of graphical methods in calculus. By plotting functions on a graph‚ students can observe key characteristics such as domain‚ range‚ intercepts‚ and asymptotes. This approach helps in understanding the behavior of functions‚ including continuity‚ differentiability‚ and periodicity. Graphical tools like graphing calculators or software enable precise visualization‚ allowing learners to explore how functions change and interact. For instance‚ plotting a function and its derivative side by side reveals their relationship. Techniques such as zooming‚ tracing‚ and analyzing transformations further enhance comprehension. Visualizing functions also aids in identifying maxima‚ minima‚ and inflection points‚ which are critical in optimization problems. This method bridges the gap between algebraic expressions and their real-world implications‚ making abstract concepts more tangible and accessible for students.
Analyzing Limits and Derivatives Through Graphs
Graphical methods provide powerful tools for analyzing limits and derivatives‚ offering visual insights into function behavior. By examining graphs‚ students can determine limits by observing the function’s approach to specific points. For instance‚ identifying holes or vertical asymptotes helps clarify limit behavior. Derivatives‚ representing the slope of the tangent line‚ can be approximated graphically using secant lines and their convergence. Graphing calculators and software enable precise exploration of these concepts. Visualizing functions and their derivatives side by side enhances understanding of rates of change. This approach simplifies complex ideas‚ making them more intuitive and accessible for learners. Graphical analysis is particularly effective for identifying key features like increasing/decreasing intervals and concavity‚ which are essential in calculus.

Numerical Methods in Calculus
Numerical methods provide approximations for derivatives‚ integrals‚ and solutions to differential equations‚ offering practical tools for solving complex calculus problems efficiently and accurately.
Approximating Derivatives and Integrals
Numerical methods are essential for approximating derivatives and integrals‚ especially when exact solutions are challenging to obtain. Techniques like Euler’s method and the trapezoidal rule provide practical tools for estimating these values. These approximations are vital in real-world applications where precise analytical solutions are difficult or time-consuming to compute. By leveraging numerical approaches‚ students and professionals can gain insights into the behavior of functions and solve complex problems efficiently. This methodological blend of accuracy and practicality underscores the importance of numerical calculus in various scientific and engineering disciplines. The ability to approximate derivatives and integrals numerically complements algebraic and graphical methods‚ offering a well-rounded problem-solving strategy. This approach is particularly valuable in modeling dynamic systems and analyzing data.
Euler’s Method for Solving Differential Equations
Euler’s method is a numerical technique for solving ordinary differential equations (ODEs) with a given initial value. It approximates the solution by using the derivative at a point to estimate the function’s value at a nearby point. This iterative process involves calculating the slope at each step and updating the function’s value accordingly. Euler’s method is straightforward to implement‚ making it a valuable tool in numerical calculus. However‚ its accuracy depends on the step size‚ with smaller steps generally yielding better approximations but increasing computational effort. Despite its simplicity‚ Euler’s method is widely used in various fields‚ including engineering and physics‚ for modeling dynamic systems and solving complex problems where exact solutions are difficult to obtain. Its practicality and ease of application make it a foundational technique in numerical analysis and scientific computing.

Algebraic Methods in Calculus
Algebraic methods in calculus provide precise formulations and solutions‚ solidifying conceptual understanding. They complement graphical and numerical approaches‚ offering exact results and enhancing problem-solving through the Rule of Four.

Solving Equations and Solidifying Conceptual Understanding
Algebraic methods in calculus are essential for solving equations with precision‚ enhancing conceptual understanding. These techniques provide exact solutions‚ complementing graphical and numerical approaches. By focusing on algebraic formulations‚ students can explore foundational concepts like continuity‚ limits‚ and derivatives in depth. This methodical approach not only aids in solving complex problems but also strengthens the ability to interpret and apply calculus principles effectively. The integration of algebraic methods with graphical and numerical techniques ensures a comprehensive grasp of mathematical relationships‚ making them indispensable in advanced problem-solving scenarios.
Antidifferentiation and Precise Formulations
Antidifferentiation is a cornerstone of calculus‚ enabling the discovery of functions whose derivatives are known. This algebraic process is vital for solving integrals and differential equations‚ providing precise mathematical formulations. By mastering antidifferentiation‚ students can reverse differentiation‚ unlocking solutions to various problems in physics‚ engineering‚ and economics. The algebraic approach offers exact results‚ contrasting with numerical approximations‚ and ensures a deep understanding of function behavior. Through precise formulations‚ calculus concepts become tangible‚ allowing for accurate modeling and analysis of real-world phenomena.
Blending graphical‚ numerical‚ and algebraic techniques enhances understanding and problem-solving in calculus. Each method complements the others‚ providing a robust framework for mastering complex mathematical concepts effectively.
Enhancing Understanding Through Multiple Representation Methods

Utilizing multiple representation methods—graphical‚ numerical‚ and algebraic—fosters a deeper comprehension of calculus concepts. By integrating these approaches‚ students can visualize functions‚ approximate solutions‚ and derive precise formulations. This multi-faceted learning strategy aligns with the Rule of Four‚ emphasizing the interconnectedness of different problem-solving techniques; For instance‚ visualizing a function’s graph alongside numerical approximations and algebraic expressions provides a holistic understanding. Such blending of methods not only enhances analytical skills but also prepares students for real-world applications‚ where problems often require diverse approaches. This comprehensive learning framework ensures a well-rounded mastery of calculus‚ making it accessible and engaging for learners at all levels.